Grafici e tabelle: quinta puntata statistica
Tabelle e Grafici: strumenti della statistica. Tabelle e grafici sono importanti strumenti che accompagnano le distribuzioni, esaminate nei contributi precedenti Le Distribuzioni Multiple. Vediamoli più da vicino. Completiamo innanzitutto la trattazione delle tabelle a doppia entrata, introducendo le tre categorie entro le quali possono essere ricomprese. Abbiamo dunque tabelle che mostrano la contemporanea rilevazione, su […]
Tabelle e Grafici: strumenti della statistica.
Tabelle e grafici sono importanti strumenti che accompagnano le distribuzioni, esaminate nei contributi precedenti Le Distribuzioni Multiple. Vediamoli più da vicino. Completiamo innanzitutto la trattazione delle tabelle a doppia entrata, introducendo le tre categorie entro le quali possono essere ricomprese. Abbiamo dunque tabelle che mostrano la contemporanea rilevazione, su un’unità statistica, di:
- 1) due mutabili;
- 2) una mutabile insieme ad una variabile;
- 3) due variabili.
Nel primo caso, prendendo al contempo due caratteri qualitativi (per approfondimenti, vedi anche Mutabili statistiche ) parliamo di tabelle di contingenza.
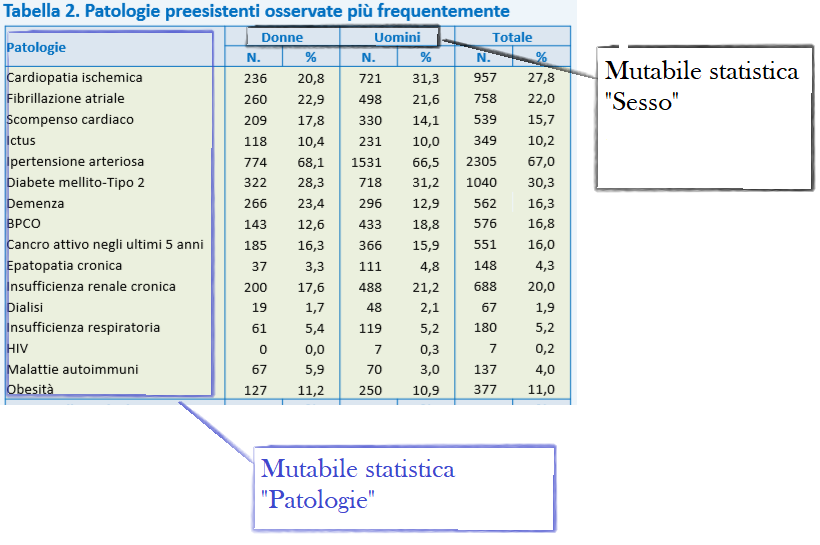
La seconda specie è invece un “ibrido” che manifesta parallelamente una carattere quantitativo ed uno qualitativo. Viene denominata anche tabella mista.
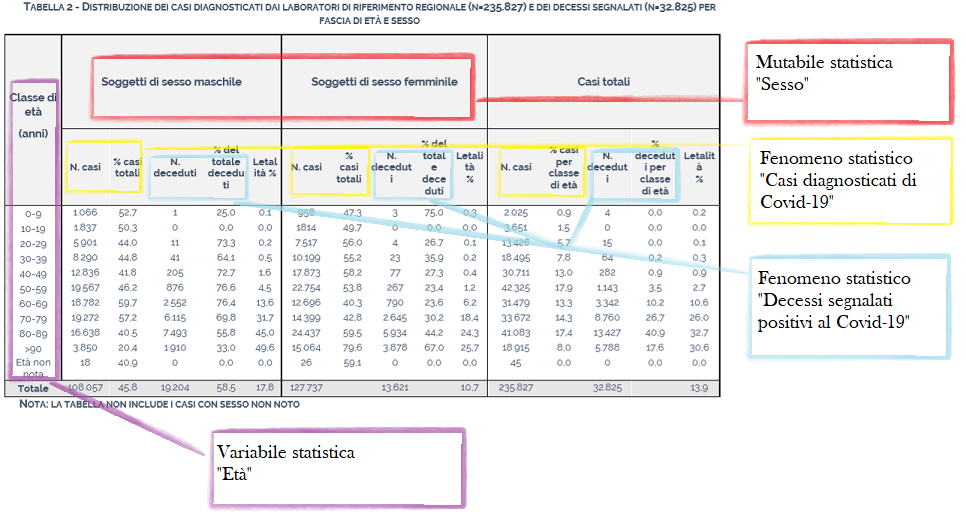
Infine esaminiamo il terzo tipo, in cui abbiamo simultaneamente due caratteri quantitativi, definita pure tabella di correlazione. Qui diamo come esempio una tabella a doppia entrata un po’ atipica, presa da un esempio scolastico.
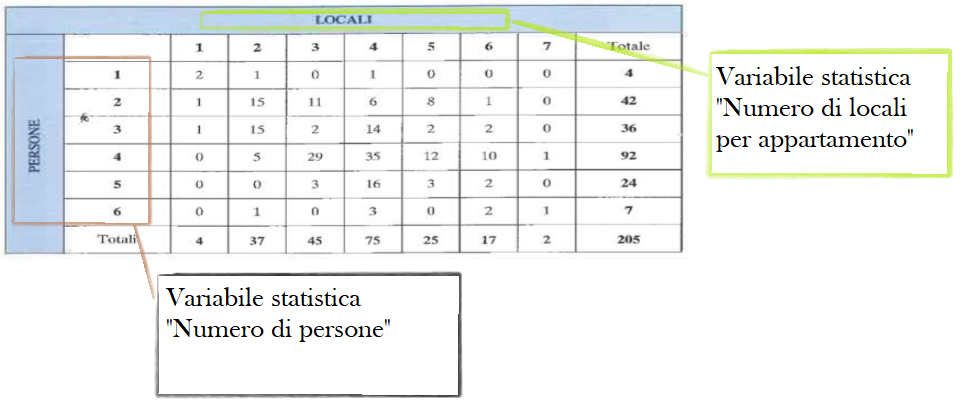
La duttilità delle tabelle, prese come singolo strumento grafico, ci consente inoltre di porre in essere altre combinazioni oltre a quelle già viste. Ad esempio, è possibile rappresentare contemporaneamente due fenomeni oggetto d’indagine, sia per quanto riguarda le distribuzioni semplici, sia per le distribuzioni doppie. Nel primo caso abbiamo una tabella strutturata come qui sotto:
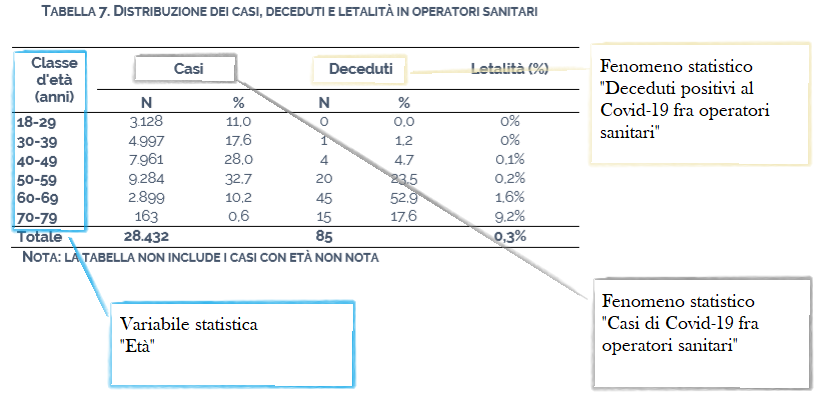
Nella seconda casistica invece abbiamo una tabella a doppia entrata di questo genere:
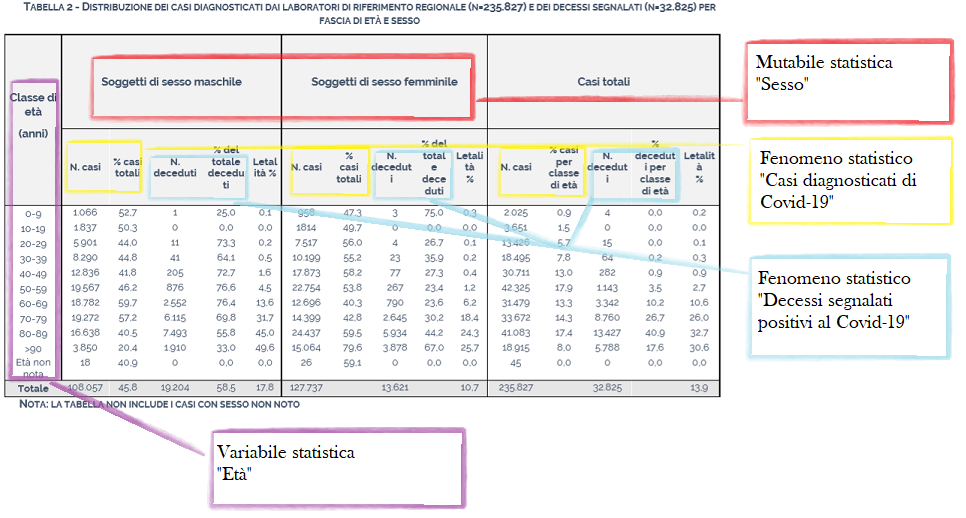
Dunque arricchiamo in maniera decisa la nostra ricerca, comparando anche diverse popolazioni n ognuna afferente ad una certo fenomeno osservato. Dunque è possibile unire i risultati di più indagini statistiche, e confrontare qualitativamente e quantitativamente due fenomeni e due distribuzioni statistiche.
Rendiamo in questo modo giustizia alla ricerca di correlazioni e dipendenze, fra vari eventi elementi coinvolti in una manifestazione reale, come ad esempio un’epidemia. Nelle tabelle trovano posto, come possiamo evincere da un’attenta lettura, anche indici e altri rapporti, che verranno definiti ed analizzati nei prossimi contributi.
Le rappresentazioni grafiche.
Quasi sempre l’elaborazione dei dati si evolve, dopo la costruzione delle tabelle, in grafici. Il ruolo di quest’ultimi è quello di “tradurre” in maniera più efficace ed immediata le informazioni contenute nelle tabelle. Dunque con i grafici non sostituiamo le tabelle, ma sono strumenti complementari ad esse in grado di “dar vita” ai loro numeri, in special modo per quelle più ampie e complesse.
Valutiamo dunque come importante il valore aggiunto che forniscono i grafici sulla comunicazione e comprensione dei dati, specialmente nell’esposizione verso il grande pubblico non sempre specializzato in materia. Pertanto è di fondamentale importanza predisporre rappresentazioni grafiche di facile lettura e non troppo complessi. Nell’eventualità di una grande mole di dati, è preferibile suddividere le caratteristiche delle mutabili/variabili rilevate in più grafici affiancati, con l’accompagnamento di note esplicative.
I grafici sono basati sostanzialmente su una proporzionalità fra le frequenze (assolute, relative o percentuali) e delle grandezze geometriche come aree o lunghezze che vengono utilizzate per rappresentare il fenomeno. Non esistono regole fisse e generali per la scelta della rappresentazione grafica con cui sintetizzare una distribuzione. Dunque è compito dell’operatore statistico scegliere la rappresentazione grafica più opportuna al fenomeno indagato.
Nel mostrare le varie tipologie di grafici possibili, per semplicità focalizziamo la relazione fra tipo di grafico e tipologia di carattere (variabile o mutabile).
Grafico a torta.
Certamente la più comune rappresentazione grafica in cui ci imbattiamo è il diagramma circolare, detto anche a torta o aerogramma. I diagrammi circolari vengono utilizzati maggiormente per presentare i risultati delle mutabili statistiche e delle variabili statistiche discrete. Un grafico a torta è formato da un cerchio, avente il raggio unitario r=1 per convenzione. I valori delle frequenze assolute, relative o percentuali corrispondono invece a precise aree in cui viene suddiviso questo cerchio.
Queste superfici “a spicchio” sono chiamate settori circolari, le cui ampiezze degli angoli al centro sono sempre proporzionali alle frequenze stesse. L’ampiezza dell’angolo al centro (αk) del settore circolare scelto per rappresentare la frequenza assoluta, relativa o percentuale di una modalità, è determinata dalla proporzione: 360°: n =αi: ni (dove n è la frequenza totale , mentre ni è la singola frequenza di una modalità).
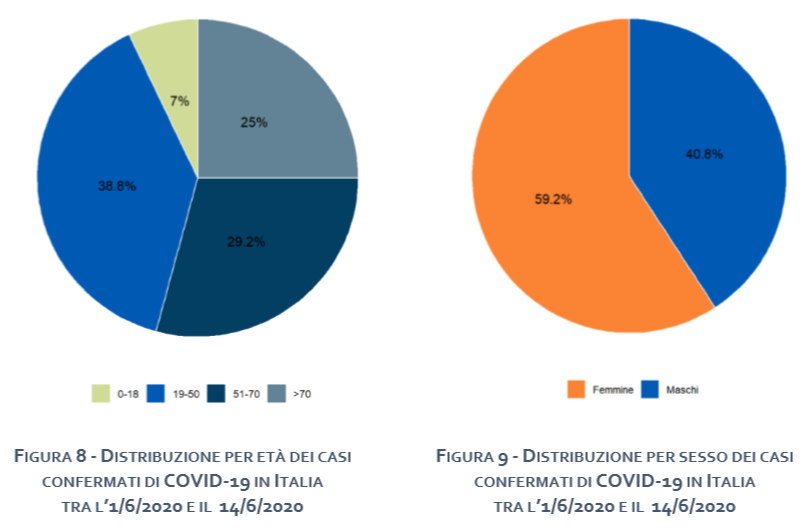
Per determinare le ampiezze degli angoli al centro, per ciascuna delle modalità osservate, è sufficiente applicare elementare aritmetica. Pertanto basta moltiplicare le frequenze di ciascuna modalità per la costante 360°:N. Diamo alcuni esempi. Qui sotto abbiamo a sinistra ed in basso una variabile statistica discreta. A sinistra invece una mutabile statistica di tipo sconnessa.

Qui invece abbiamo una mutabile statistica ordinata, ovvero “Stato clinico attuale”, in cui per sottolinearne l’ordinamento generale presente vengono adottate specifiche accortezze.
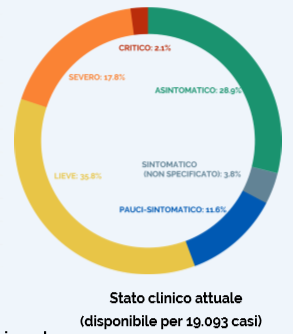
Sono visibili non a caso delle gradazioni di colore che man mano diventano di intensità sempre più crescente, accompagnate da delle nomenclature specifiche, per sottolineare la severità e l’importanza dei sintomi riscontrati sulle unità statistiche.
Grafico a barre.
Il secondo tipo di grafico è il diagramma a barre (o a strisce), detto anche ortogramma. Esso è costituito da un insieme di rettangoli, solitamente non adiacenti fra di loro ma equidistanti. Ogni barra corrisponde ad una singola modalità, ed assume una base di dimensione costante ed unitaria b=1. L’ altezza è invece proporzionale ad una frequenza assoluta, relativa o percentuale della modalità stessa. Dunque l’area di ogni singola barra equivale ad una determinata frequenza associata ad una certa modalità.
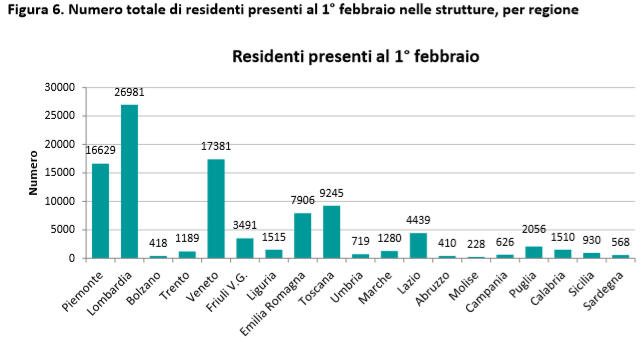
Sono presenti tanti rettangoli quante sono per l’appunto le modalità/classi. I diagrammi a barre sono di due tipi: a colonne, se il grafico si sviluppa su un asse verticale; a nastri, se invece si sviluppa su un asse orizzontale. Vediamo un diagramma a colonne.
Ed uno a nastro:
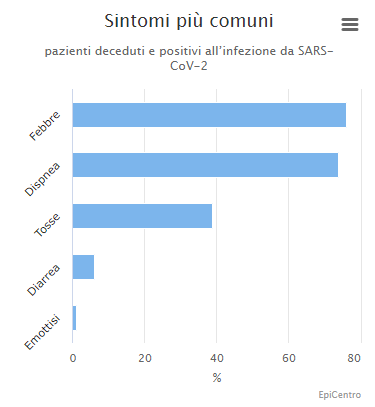
Per le sue caratteristiche, il diagramma a barre è usato nella rappresentazione grafica di mutabili statistiche, ma anche per variabili statistiche discrete come qui sotto.
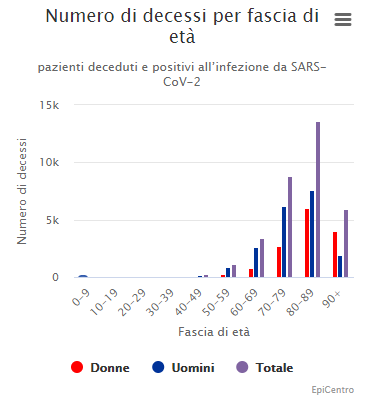
Come notiamo, nel diagramma a barre possiamo confrontare anche l’andamento di più caratteri contemporaneamente. Infatti nel caso precedente vediamo una distribuzione statistica doppia in cui come riferimento di base abbiamo la variabile “Età”, in concomitanza alla mutabile “Sesso”. Naturalmente lo stesso principio vale in presenza di due mutabili, come qui in figura:
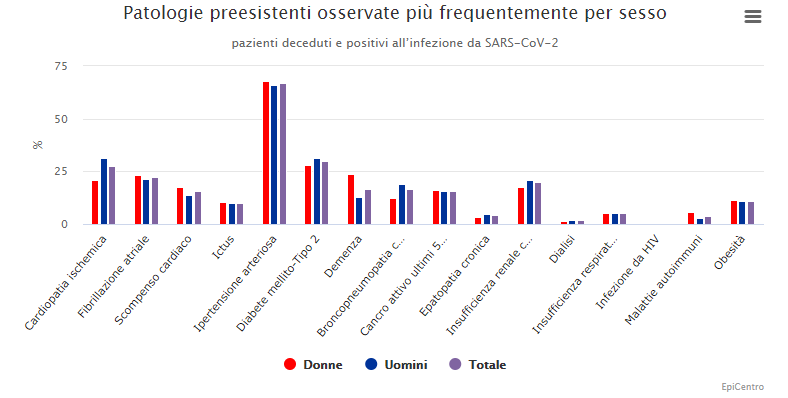
Pertanto il diagramma a barre può essere utilizzato anche nella spiegazione di distribuzioni statistiche doppie.
Cartogramma.
Come ulteriore tipologia di grafico, abbiamo il cartogramma. È un grafico diverso, che si avvale di mappe rappresentanti l’area geografica in cui rileviamo il fenomeno oggetto d’indagine. Le cartine geografiche sono generalmente politiche (mostrano solo i confini di un’unità territoriale) e spesso mute (non sono presenti nomi di località). Comunque, non è esclusa l’indicazione delle regioni o capoluoghi più importanti.
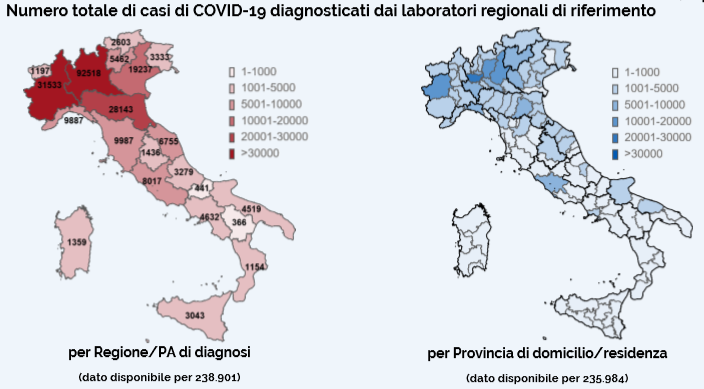
Ogni unità geografica è colorata secondo una gradazione di colore differente, relazionata all’intensità del fenomeno su cui si conduce l’indagine. Più il colore è scuro e cupo, maggiore è la frequenza del fenomeno in quella specifica parte del territorio. Viceversa, a sfumature più tenui e chiare corrispondono frequenze di minor rilievo. Un importante svantaggio del cartogramma è che non possono rappresentare dati molto dettagliati e precisi, a favore però di un’immediatezza di lettura notevole.
Accanto alla cartina perciò è rappresentata una scala graduata ed una legenda, con lo scopo di facilitarne l’interpretazione. Per sopperire allo svantaggio appena citato, al cartogramma possiamo aggiungere anche altri dettagli, come frequenze assolute e percentuali:
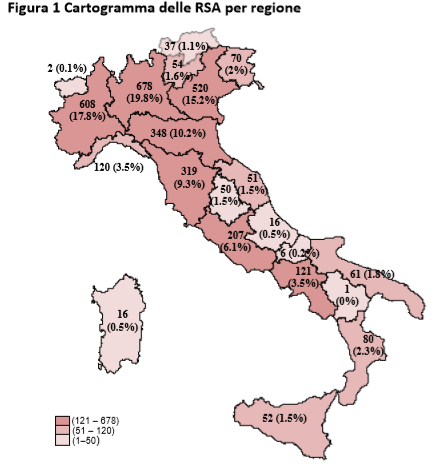
Questa tipologia di cartogramma appena mostrata viene chiamata a mosaico. Esistono anche cartogrammi a punti. In quest’ultimi è presente innanzitutto un riferimento visivo, in cui ad un cerchietto di dimensioni prefissate corrispondono delle precise frequenze, o intervalli di esse.
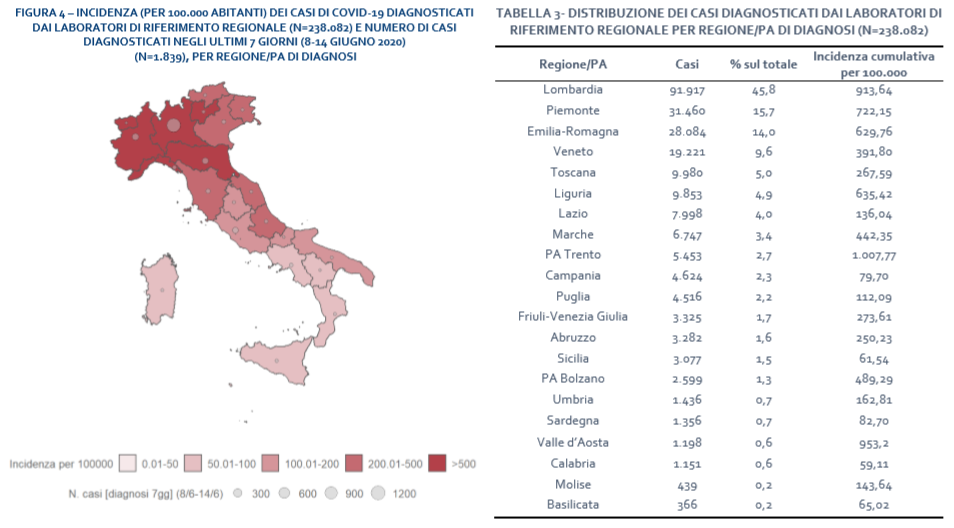
Maggiore è il diametro, e dunque le dimensioni, del cerchietto, maggiore è l’intensità del fenomeno che vogliamo dimostrare, e viceversa. Come in figura sopra, il cartogramma a punti può essere utilizzato in associazione ad uno a mosaico, specialmente quando vogliamo valutare fra di loro ed allo stesso tempo due distinti fenomeni.
Leggi anche: Le distribuzioni multiple: quarta puntata nella statistica




No Comment! Be the first one.