Mutabili Statistiche |la Terza Parte della Guida alla Statistica
Mutabili statistiche è la terza parte della guida alla Statistica proposta sulle pagine de Il Progresso Magazine. Continuiamo la nostra esposizione dei principali argomenti che riguardano questa affascinante disciplina, in vista del difficile periodo storico che tutti noi stiamo vivendo.
Un pò di chiarezza ci vuole! Vedi anche l’articolo introduttivo Statistica e Coronavirus: guida ai dati quotidiani .
Approfondimenti sulla nozione di intervallo di classe
Negli ultimi paragrafi del contributo COVID-19 e Statistica: Seconda parte abbiamo introdotto alcune informazioni sul concetto di intervallo di classe. Completiamo il quadro aggiungendo alcune osservazioni in merito.
Generalmente l’ampiezza degli intervalli di classe (a) è costante. Contengono cioè lo stesso numero di modalità del carattere. Può anche capitare il contrario, presentando una diversa ampiezza (a) come nella tabella 3 seguente.
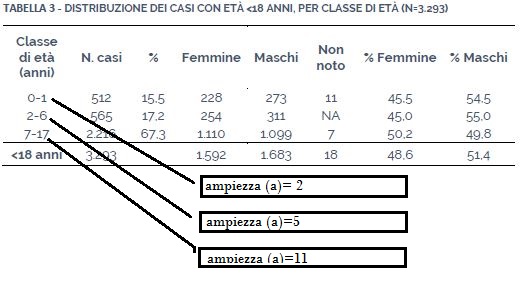
In aggiunta, molto spesso l’ultimo intervallo di classe viene lasciato aperto, ovvero senza un limite superiore. Con riferimento alla tabella dell’articolo precedente, nel fondo scala possiamo vedere un intervallo finale “fascia d’età “>90” .
Le motivazioni nel predisporre intervalli d’ampiezza differente da un lato e di intervalli finali “aperti” dall’altro hanno un loro perchè. In dettaglio, risiedono nell’evitare uno o più intervalli di classe vuoti.
Intervalli di classe che dunque non hanno o nessuna frequenza rilevata, oppure bassissima e dunque trascurabile. Questo accade sempre in virtù di una più agevole comprensione delle tabelle riassuntive di distribuzione di frequenza semplice.
Conclusioni sul concetto di classe
Nella definizione degli intervalli di classe bisogna anche avere particolare cura sulla precisione dei limiti inferiori e superiori. E’ importante che abbiano i giusti “stacchi” e non presentino sovrapposizioni ed ambiguità.
Avere infatti una tabelle costruita ad esempio nel seguente modo, potrebbe creare sconcerto!
| Fascia d’età | Frequenza assoluta | Frequenza relativa | Frequenza percentuale |
| 10-19 | 5 | …. | …. |
| 19-29 | 28 | … | … |
Una frequenza della modalità “19”, in quale rigo andrebbe inserita? In tutt’e due creerebbe una duplicazione dei dati che falserebbe inesorabilmente l’indagine!
Dunque sarebbe corretta l’impostazione seguente:
| Fascia d’età | Frequenza assoluta | Frequenza relativa | Frequenza percentuale |
| 10-19 | 4 | …. | …. |
| 20-29 | 27 | … | … |
In funzione di ciò, è importante stabilire anche quanti intervalli di classe adottare. Come già affermato, avere troppe classi è un problema, ma lo è anche averne poche.
A livello empirico, il numero di classi (k) è compresa fra 5 e 15, fino ad arrivare a 20 per popolazioni statistiche di numerosità (n) considerevole.
Nel nostro caso, (vedi tabella “Fascia d’età”), chi ha predisposto le statistiche ha scelto k=10, quindi 10 fasce d’età di ampiezza a=10 tranne l’ultima, che come visto rimane di ampiezza indeterminata in quanto “aperta”.
Piccola ricapitolazione
Fino ad ora abbiamo parlato delle variabili statistiche discrete. Avvisiamo il lettore che gli stessi principi governano anche le variabili statistiche di tipo continuo. Anzi, in verità, le varie particolarità sull’intervallo di classe sono estensioni alle variabili discrete di concetti che ben si adattano nei confronti delle variabili continue.
Dunque riteniamo opportuno per ora trascurare quest’ultime, per ragioni di semplicità.
Ci siamo limitati ad affrontare nello specifico solo distribuzioni statistiche semplici, perciò indagini con l’interesse posto su un solo carattere statistico. Seguiremo allora lo stesso canone per le mutabili statiche.
Le fasi che contraddistinguono il trattamento di una mutabile sono simili a quelle di una variabile statistica. Pertanto è possibile compiere la predisposizione di distribuzioni unitarie semplici, e successivamente la loro trasformazione in distribuzioni di frequenza semplici.
Quindi il lettore potrà agevolmente confrontare i successivi paragrafi con il contributo precedente per avere le idee chiare sul trattamento delle mutabili.
Le mutabili statistiche
Come già detto in precedenza, le mutabili statistiche sono caratteri qualitativi, nei quali non trattiamo più “modalità-numeri”, ma” modalità-attributi, sostantivi, aggettivi”.
Le mutabili statistiche possono essere suddivise in varie tipologie. Parliamo di mutabile statistica sconnessa, quando fra le varie modalità di manifestazione del carattere non possiamo stabilire un ordine naturale o precostituito di successione.
Di conseguenza costruiamo una c.d. scala nominale. Esempi di mutabili sconnesse sono la regione d’appartenenza, il sesso etc.
La mutabile statistica ordinata riguarda modalità del carattere che assumono un ordinamento naturale di precedenza l’una rispetto all’altra, crescente o decrescente.
Ebbene, instauriamo così una c.d. scala ordinale. Citiamo come esempio di mutabili ordinali il titolo di studio, qualifiche aziendali etc.
La mutabile statistica sconnessa
Riprendiamo il fenomeno esposto nell’articolo scorso, ovvero relativo ai deceduti e positivi all’infezione da COVID-19 fra i pazienti italiani. Ora, non vogliamo saperne di più sul carattere “età al momento del decesso”, ma sul carattere “regione del decesso”.
Qui sotto riportiamo una distribuzione statistica semplice di stampo geografico. La numerosità del collettivo statistico è leggermente aumentata rispetto a prima, raggiungendo n= 29.692.
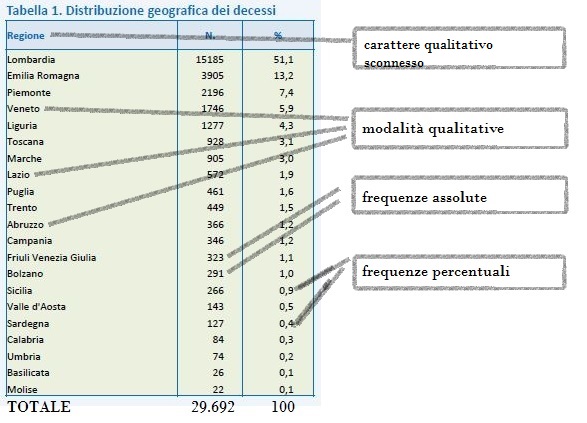
Il concetto di regione qui assume una valenza meramente territoriale. Pertanto non avrebbe senso parlare di una maggiore importanza della “Lombardia” rispetto al “Molise”.
Spieghiamoci meglio. Non c’è un preciso parametro concettuale di riferimento per stabilire Lombardia>Molise, a differenza dei caratteri quantitativi numerici già affrontati, in cui è possibile accertare ad esempio 85>68, o 56>42.
Lombardia e Molise sono nella loro essenza entrambe regioni a statuto ordinario, poste sullo stesso livello giuridico. Invece 85 è maggiore di 68 per principio matematico, cosi come 56 è maggiore di 42.
Le modalità “nomi di regione” sono classificate in base alle frequenze registrate di casi COVID-19, in ordine decrescente. Attenzione agli inganni, non è una contraddizione su quanto esposto finora!
E’ una pura scelta convenzionale ai fini di leggibilità immediata e comprensione della tabella. Nulla vieta infatti di porre in prima posizione la Sardegna, 17-esima, oppure la Puglia 11-esima, e la Lombardia come 18-esima etc.
Poichè dobbiamo pur cominciare ad elencare le regioni in qualche modo, adottiamo un criterio supplementare. Potrebbe essere un ordine alfabetico, o l’estensione territoriale, o il numero di abitanti e via dicendo.
La tabella non cambierebbe minimamente nel suo spirito, anche se magari forse diventerebbe più confusa, seppur validissima.
Raggruppamento della mutabile statistica
Quanto detto nel paragrafo appena terminato vale in toto anche per quest’altro esempio successivo di mutabile sconnessa. Qui è più evidente la casualità dell’ordinamento delle modalità.
Un luogo di esposizione al contagio infatti non è valutato più importante rispetto all’altro. Le modalità sono ordinate, come prima,in ordine decrescente di frequenza solo per pura convenzione.
Di solito per ogni singola modalità qualitativa viene definita una specifica singola classe in cui si associano le rispettive frequenze. Ma è anche possibile un’aggregazione delle modalità, sebbene ciò avviene meno frequentemente rispetto alle variabili.
Più modalità della formulazione originaria, che hanno fra di loro un fattore di fondo comune, vengono fuse insieme in un’unica classe. La fusione avviene sempre sommando fra di loro le singole frequenze associate alle singole “modalità-attributi, sostantivi, aggettivi”.
I gruppi omogenei
Ci troviamo davanti ad un processo analogo al raggruppamento in intervalli di classe come avviene nelle variabili numeriche, anche se nelle mutabili statistiche parliamo più propriamente di gruppi omogenei.
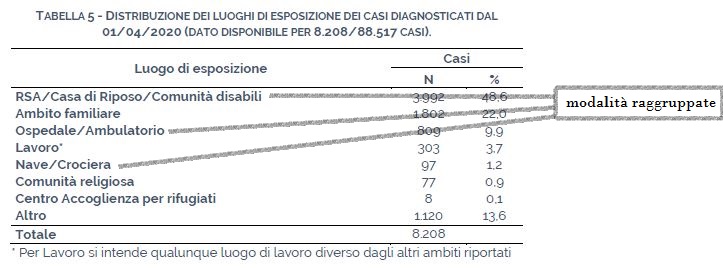
A livello operativo abbiamo le stesse tipologie di azioni, seppure con le dovute differenze. Inoltre anche nelle aggregazioni di mutabili perdiamo una certa quantità di informazioni nel dettaglio dei dati, a vantaggio però di una maggiore percezione delle tabelle.
“RSA”, “Casa di Riposo”, e “Comunità disabili” sono tre luoghi differenti e dunque tre modalità distinte, ed ognuna in teoria dovrebbe avere singolarmente nel dettaglio delle precise frequenze. Ad esempio (per pura fantasia)
| RSA | 500 | 6,09% |
| Casa di Riposo | 1492 | 18,17% |
| Comunità disabili | 2000 | 24,36% |
Ma essendo accomunate nell’essere tutte e tre strutture assistenziali, per una maggiore chiarezza è stata decisa la loro unione in un unico gruppo omogeneo di modalità.
Sommando le singole frequenze assolute di ogni singola modalità dettagliata otteniamo 500+1492+2000 = 3992. Ugualmente per le singole frequenze percentuali abbiamo 6,09%+18,17%+24,36%= 48,62%, arrotondato a 48,6%.
Lo stesso discorso vale per “Ospedali” e “Ambulatori”, entrambi luoghi di cura medica e “Nave” e “Crociera“, ambedue tipologia di naviglio. Oppure nelle modalità “Lavoro” od “Altro”, ciascuna delle quali potrebbe a sua volta essere scomposta in altre centinaia di modalità più specifiche.
Alla luce di quanto detto finora, l’aggregazione nelle mutabili potrebbe sembrare più snella rispetto al raggruppamento nelle variabili.
La mutabile statistica ordinata
Vediamo ora un esempio di mutabile ordinata.
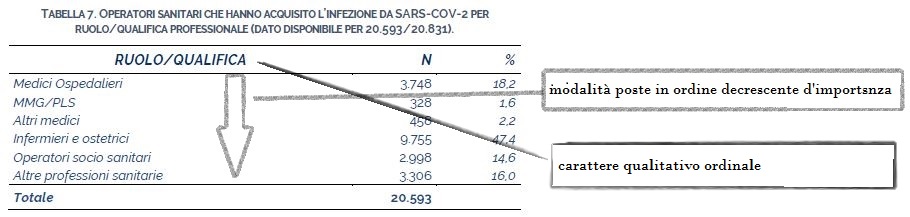
Qui l’ordinamento delle modalità avviene secondo uno schema precostituito. Infatti vengono posizionate, dall’alto in basso, le singole modalità “ruoli sanitari” secondo una sistemazione in linea generale di tipo gerarchica.
Dai medici ospedalieri, passando per infermieri e ostetrici, e poi attraverso gli OSS viene percorso l’organigramma tipico di un’azienda sanitaria e del SSN.
Ogni categoria superiore ha, nei confronti di quella inferiore, precisi poteri direttivi e una posizione contrattuale superiore, dettate da varie fonti del diritto civile.
A controprova di ciò, vediamo che scompare il criterio convenzionale della disposizione secondo frequenze decrescenti. Lasciamo dunque spazio per l’appunto all’ordinamento naturale, nella sua essenza, della precisa mutabile ordinale “ruolo/ qualifica”.
Leggi anche: COVID-19 e Statistica: Seconda parte
